《数独与幻方》

    新年伊始，《北京晚报》的公众平台版推出了“数独”专栏，每天刊载初、中、高三个级别的数独游戏。 

    “数独”这个词来自于日语，我不懂日语，但知其对应的英语是sudoku，从发音看是日语的音译，其含意是“只出现一次的数字”，也就是单独的数字，翻成中文后，变成了专有名词——数独。

    据说这个游戏最早起源于欧洲，20世纪80年代在日本广为流行，随后蔓延到全世界，形成了在数字间玩乐的热潮。在许多国家和城市，“数独”成为报纸、书刊、电视节目中的一个专栏，互联网上也有不少“数独”的专门网站。“数独”逐渐成为一种消闲文化，成为人们自娱自乐的休闲方式。

    数独游戏由9个“九宫格”组成一个9行9列的方块，内有81个方格，在一些方格中预先设定了1至9之间的数字，玩者需要在空格内填上1至9之间的剩余数字，使每1行，每1列，每1个九宫格都有1至9的数字，不能有重复的数字出现。

    这个游戏看似简单，不需要丰富的知识，也没有任何计算，但却需要慎密的思考与推理。成人可以玩，儿童也可以玩，适合各种年龄层次，老少咸宜。在玩乐中，锻炼着分析、推理的能力。

    2006年3月10-11日，第一届数独世界锦标赛在意大利的卢卡举行，31岁的捷克女选手亚娜·季洛娃过关斩将成为全球的首位数独冠军。

    数独，这个游戏的形式使我想到了幻方。

    数独的基本单元是九宫格，而九宫格恰好是一个三阶幻方。我想，这个游戏说不定是由三阶幻方衍生出来一种玩法。幻方是数学中一个特定的研究对象，蕴含着很深奥也很复杂的数学现象。

    第一次接触幻方，还是在小学四年级的时候。邻居家有位大学生，我常去找他做些智力题，一次，他画了一个3行3列有9个格子的方块，让我填上1-9，使每行每列及对角线上的数字和都相等，这个好做，很快我就做出了答案。他又画出一个5行5列有25个格子的方块，让我填上1-25，使每行每列及对角线上的数字和都相等，这个就有些难了，试填了许久也没有做出来。随后，他教给我怎样填写的方法，按照他讲的方法，任何奇数行列的格子都能填写出来，但偶数行列的格子不适用，他也不会。那时，我还不知道这样的格子叫“幻方”。

    进入中学以后，我常去首都图书馆看书，在那里，我知道了这种行列组成的格子叫幻方，英文是magic square，里面蕴藏着许多深奥的数学现象。我还知道了幻方是我们中国人首先发现的，后来经印度传到了欧洲。

    早在大禹治水时，在洛水见到一只大龟，龟背上有一幅奇特的图案。

    用现在的数学符号表示，就是一个最简单的3阶幻方。

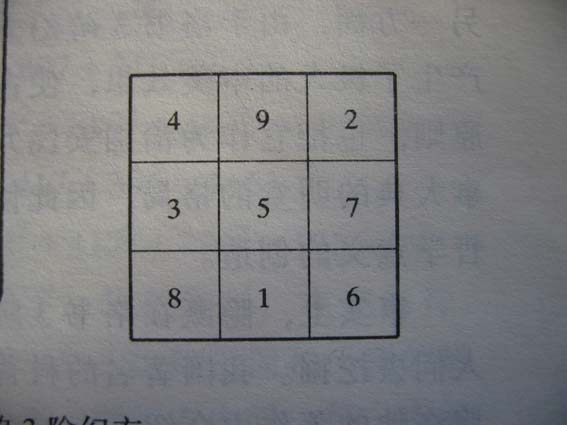
    它的每行每列及两条对角线上的数字和都是15。这就是世界上最早出现的幻方。

    南宋时期的数学家杨辉对幻方做过大量的研究，从3阶到10阶幻方都有详细的论述，在世界数学史上留下了光辉的一页。

    幻方看似简单，其表象人人都可以理解，但却蕴含着许多至今无人能够解答问题。幻方是数学的一个重要分支——组合学的基础。

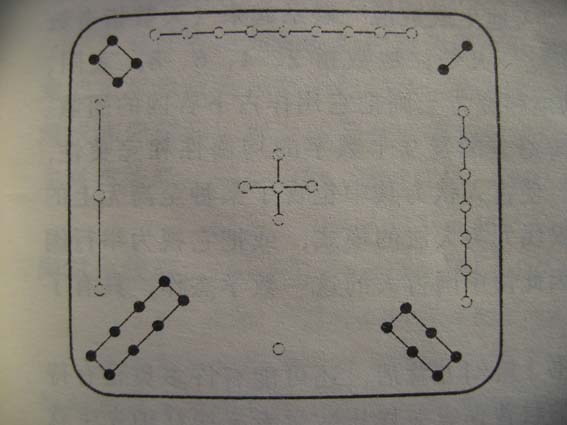
    如果你玩过扑克游戏，可能会接触到这个图案。

    确切地讲，它不是幻方，名为拉丁方，英文叫latin square。

    这个扑克组成的图案，也是非常奇特。它的每行4张、每列4张、对角线4张、每角4张及中央4张都包含着两个元素，一个是扑克牌的花色，另一个是扑克牌的点数。

    数学就是这样神奇，这个研究现实世界里数量关系与空间图形的学科不少人都不喜欢，觉得枯燥乏味，其实数学渗透在生活的方方面面，它的乐趣与美感只有在对它的探索中才能获取。